SMALL
[수학2] 함수의 극한과 연속 - 01 함수의 극한
안녕하세요, 오늘은 수학2의 함수의 극한과 연속에 대해 이야기해보려 합니다. 우선, 함수의 극한부터 차근차근 알아봅시다.
먼저, 극한이란 무엇일까요? 간단히 말해, 극한이란 함수의 특정한 점에 근접할 때 함수의 값을 의미합니다. 여기서는 리미트라는 기호를 사용해 표현합니다. 함수의 극한에서는 두 가지 경우를 주로 다룹니다.
하나는 수렴하는 경우, 다른 하나는 발산하는 경우입니다. 수렴하는 경우는 함수의 값이 특정한 숫자로 점점 가까워지는 것을 의미하며, 발산하는 경우는 함수의 값이 양의 무한대나 음의 무한대로 점점 멀어지는 것을 말합니다. 문제를 풀 때는 이러한 개념을 이해하고 적용해야 합니다.

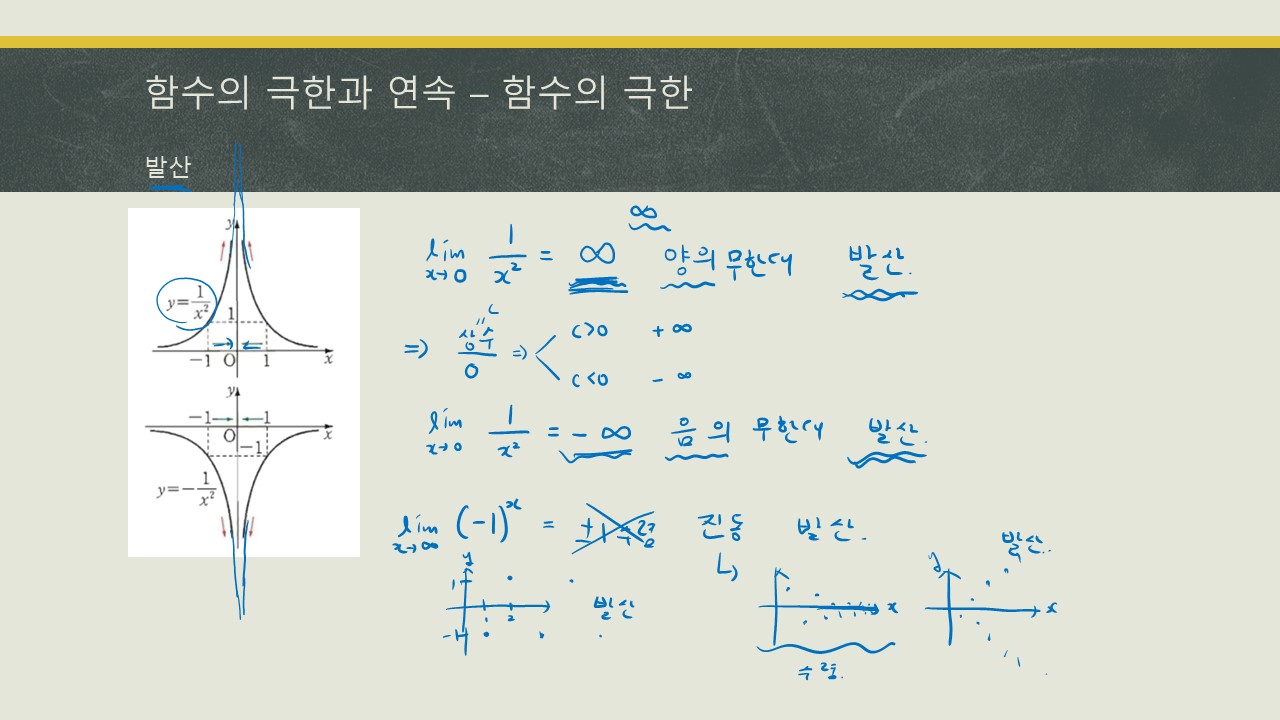





무한대 분에 무한대 형태일 때, 최고차항으로 나눠주고 푸는 것이 정확한 풀이입니다.
그러나 문제를 빠르게 풀 때는 분모분자의 차수를 비교하여 분자가 크면 발산, 분모가 크면 0으로 수렴하고, 분모분자가 같으면 계수비를 이용해서 풀 수 있습니다. 또한, x가 음의 무한대로 갈 때는 -t로 치환하는 것이 헷갈리지 않습니다.
변수를 변형할 때에는 주의가 필요하며, 다른 형태의 문제도 위에서 설명한 형태로 바꾼 뒤 풀면 됩니다. 좀 더 세부적인 설명과 문제 풀이는 다음 포스팅에서 계속될 예정입니다.
오늘 배운 내용을 복습하고, 다음 내용을 기대해주세요!
LIST
'공부' 카테고리의 다른 글
| 직무교육에 대해서 알아보기 (0) | 2024.03.04 |
|---|---|
| 중고차 구매시 사기 방지 방법 (0) | 2024.03.02 |
| 수학2 개념 설명 전 목차 설명 (0) | 2024.02.25 |
| 가벼운 대학생 노트북 추천 LG 그램 14인치 (1) | 2024.02.23 |
| 수학의 한 분야인 '미분'에 대한 이야기 (0) | 2024.02.20 |

댓글